1. 选择排序思想

插入排序（Insertion sort）是一种简单直观且稳定的排序算法。

插入排序的方式非常像我们整理扑克牌一样。我们每次拿起一张牌并将它插入牌中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较，如下图所示：

2. 选择排序详解

排序原理：

1. 把所有的元素分为两组，已经排序的和未排序的；
2. 找到未排序的组中的第一个元素，向已经排序的组中进行插入；
3. 倒叙遍历已经排序的元素，依次和待插入的元素进行比较，直到找到一个元素小于等于待插入元素，那么就把待 插入元素放到这个位置，其他的元素向后移动一位；

【排序动画演示】

---

我们拿第四趟和第五趟排序详细理解一下：

【第四趟排序】 首先待插入的数字为6，前面的4,6,7,8已经有序。我们将数字6放入到子序列4,6,7,8中合适的位置。从右向左倒序遍历4,6,7,8(因为是递增排序)，元素6先和子序列中的8比较，发现自己比8小，6和8交换位置。

交换完之后，6继续和前面的4,6,7元素逐个比较。

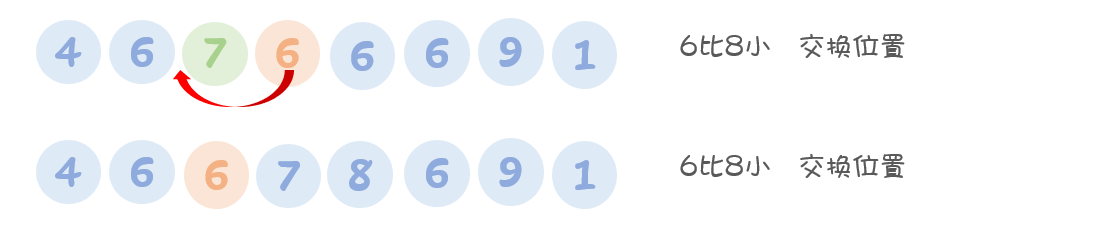
直到比较到6时，发现已经等于自己了，则此趟排序结束。

【第五趟排序】

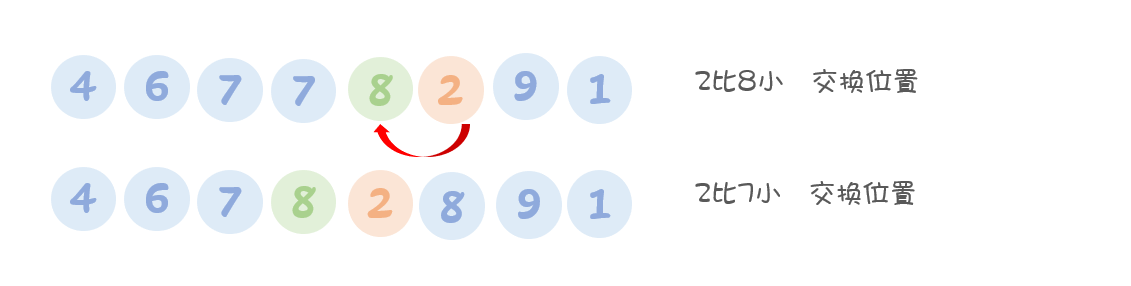
直到将2放到子序列的第一位

3. 直接插入排序代码实现

外层循环控制有序元素，内层循环实现待插入元素比较交换

public void insertSort(int[] arr) {
        // 默认第一个元素有序
        for (int i = 1; i < arr.length; i++) {
            // 待排序元素插入到已排序元素中
            for (int j = i; j > 0; j--) {
                // 将待排序元素arr[j]倒序依次与有序序列中元素比较，放入有序序列中合适位置
                if(arr[j] < arr[j-1]) {
                    int temp = arr[j];
                    arr[j] = arr[j-1];
                    arr[j-1] = temp;
                } else {
                    // 有序则不做处理(等同于break)，此处不加else也可以
                    break;
                }
            }
        }
    }

测试

[1, 2, 4, 6, 6, 7, 8, 9]

4. 折半插入排序代码实现

其实，这就是将待排序元素通过二分查找放到已有序的子序列，更快速的定位定位插入的位置。

二分查找的前提就是有序的子序列查找，折半插入排序在数据集无序的情况下要优于直接插入排序，但是在近乎有序的数据集下，由于插入排序只比较一次，因此最好情况下的直接插入排序要优于折半插入排序。

折半插入与直接插入区别： 这里的查找操作的时间复杂度为O(n)量级。但是如果使用二分查找在数组 arr 的 [0,i - 1] 的范围内查找关键字 key ，那么就可以将查找操作的时间复杂度降到O(logn)量级.

public int[] insert(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int index = binary_search(arr, arr[i]);
        for (int j = i; j > index; j--) {
            if (arr[j] < arr[j - 1]) {
                int temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
            }
        }
    }
    return arr;
}

public int binary_search(int[] arr, int target) {
    int left = 0, right = arr.length - 1;
    while(left < right) {
        int mid = (left + right) >>> 1;
        if(target > arr[mid]) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    return left;
}

测试

[1, 2, 4, 6, 6, 7, 8, 9]

5. 复杂度分析

【时间复杂度】

插入排序使用了双层for循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析内层循环体的执行次数即可。

最坏情况，也就是待排序的数组元素为逆序 {9，8，7，6，6，4，2，1}

那么：比较的次数为：(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1) * (N-1) / 2 = N^2/2-N/2;

交换的次数为：(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1) * (N-1)/2 = N^2/2-N/2;

总执行次数为：(N ^ 2/2 - N/2) + (N ^ 2 / 2-N/2)=N ^ 2 - N;

根据大O推导法则，插入排序的时间复杂度为O(N^2)

【空间复杂度】 O(1)